

If a is negative, you can multiply both sides of the equation by −1.įor example, you can multiply both sides of the equation "a" should be positiveĪlthough a can be either positive or negative, it is preferred to put the equation in the form where a is a positive number.
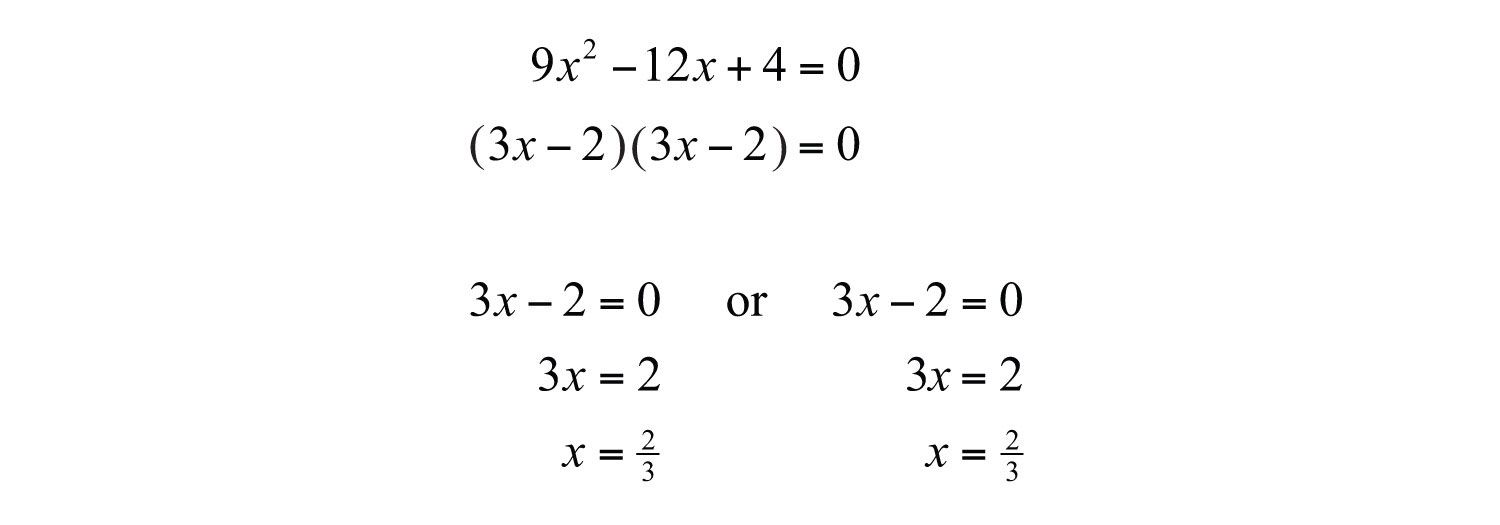
X 2 + x + 5 = 0 by subtracting x 2 − 4 from both sides of the equation.Ģx 2 − x = 7 + 3x should be put in the form of 2x 2 − 4x − 7 = 0 by subtracting 7 + 3x from both sides of the equation. The equation 3x 2 + x + 1 = x 2 − 4 should be put in the form of The expression on the right side of the equal sign must equal 0 to be in the proper quadratic equation format.

There is a definite format for the quadratic equation. ( See Linear Equations for more information.) Put in proper format The following equations are not quadratic equations, because a = 0.ģx 2 − 3x 2 + x + 5 = 0 because 3x 2 − 3x 2 = 0, resulting in x + 5 = 0 If a = 0, the equation becomes an equation of the first degree or a linear equation of the form bx + c = 0. a, b and c represent positive or negative numbersĪ quadratic equation is considered an equation of the second degree, because of the x 2 term.The quadratic equation is in the form of:


 0 kommentar(er)
0 kommentar(er)
